Next: , Previous: , Up: Available Constraints   [Contents][Index]

10.9.4.8 Placement Constraints

disjoint1(+Lines)   obsolescent
disjoint1(+Lines,+Options)

constrains a set of lines to be non-overlapping. This constraint is best replaced by diffn/[1,2] in new code.

Lines is a list of terms F(Sj,Dj) or F(Sj,Dj,Tj), Sj and Dj are domain variables with finite bounds denoting the origin and length of line j respectively, F is any functor, and the optional Tj is an atomic term denoting the type of the line. Tj defaults to 0 (zero).

Options is a list of zero or more of the following, where Boolean must be true or false (false is the default):

global(Boolean)

if true, then a redundant algorithm using global reasoning is used to achieve more complete pruning.

wrap(Min,Max)

If used, then the space in which the lines are placed should be thought of as a circle where positions Min and Max coincide, where Min and Max should be integers. That is, the space wraps around. Furthermore, this option forces the domains of the origin variables to be inside [Min,Max-1].

margin(T1,T2,D)

This option imposes a minimal distance D between the end point of any line of type T1 and the origin of any line of type T2. D should be a positive integer or sup. If sup is used, then all lines of type T2 must be placed before any line of type T1.

This option interacts with the wrap/2 option in the sense that distances are counted with possible wrap-around, and the distance between any end point and origin is always finite.

disjoint2(+Rectangles)   obsolescent
disjoint2(+Rectangles,+Options)

constrains a set of rectangles to be non-overlapping. This constraint is best replaced by diffn/[1,2] in new code.

Rectangles is a list of terms F(Xj,Lj,Yj,Hj) or F(Xj,Lj,Yj,Hj,Tj), Xj and Lj are domain variables with finite bounds denoting the origin and size of rectangle j in the X dimension, Yj and Hj are the values for the Y dimension, F is any functor, and the optional Tj is an atomic term denoting the type of the rectangle. Tj defaults to 0 (zero).

Options is a list of zero or more of the following, where Boolean must be true or false (false is the default):

global(Boolean)

Disabled.

wrap(Min1,Max1,Min2,Max2)

Min1 and Max1 should be either integers or the atoms inf and sup respectively. If they are integers, then the space in which the rectangles are placed should be thought of as a cylinder wrapping around the X dimension where positions Min1 and Max1 coincide. Furthermore, this option forces the domains of the Xj variables to be inside [Min1,Max1-1].

Min2 and Max2 should be either integers or the atoms inf and sup respectively. If they are integers, then the space in which the rectangles are placed should be thought of as a cylinder wrapping around the Y dimension where positions Min2 and Max2 coincide. Furthermore, this option forces the domains of the Yj variables to be inside [Min2,Max2-1].

If all four are integers, then the space is a toroid wrapping around both dimensions.

margin(T1,T2,D1,D2)

This option imposes minimal distances D1 in the X dimension and D2 in the Y dimension between the end point of any rectangle of type T1 and the origin of any rectangle of type T2. D1 and D2 should be positive integers or sup. If sup is used, then all rectangles of type T2 must be placed before any rectangle of type T1 in the relevant dimension.

This option interacts with the wrap/4 option in the sense that distances are counted with possible wrap-around, and the distance between any end point and origin is always finite.

synchronization(Boolean)

Disabled.

diffn(+Boxes)   since release 4.6
diffn(+Boxes,+Options)

constrains a set of multidimensional boxes to be non-overlapping.

A box is represented by a term [Facet,Facet,...]. A facet is a term of the form Origin-Length, where the domain variables Origin and Length are the coordinate and length of the box in the given dimension. All boxes should have the same dimensionality (length of the box term).

Options is a list of zero or more of the following, where Boolean must be true or false:

strict(Boolean)

If false (the default), then the constraint is true iff, for all pairs of boxes i, j, there exists a dimension with respective facets Oi-Li and Oj-Lj and their overlap is zero, i.e.: 

Oi+Li <= Oj or
Oj+Lj <= Oi or
Li = 0 or
Lj = 0

If true, then the constraint is true iff, for all pairs of boxes i, j, there exists a dimension with respective facets Oi-Li and Oj-Lj and one precedes the other, i.e.: 

Oi+Li <= Oj or
Oj+Lj <= Oi

Corresponds to diffn* and disjunctive* in MiniZinc.

bin_packing(+Items,+Bins)   since release 4.4

constrains the placement of items of given size in bins of given capacity, so that the total load of any bin matches its capacity.

Items is a list of terms of the form item(Bin,Size) where Bin is a domain variable denoting the bin where the item should be placed, and Size is an integer >= 0 denoting its size.

Bins is a list of terms of the form bin(ID,Cap) where ID is an integer identifying the bin, and Cap is a domain variable denoting is its capacity. The ID values should be all different.

The constraint holds if every Bin equals one of the ID values, and for every bin bin(ID,Cap), the total size of the items assigned to it equals Cap.

Corresponds to bin_packing* in MiniZinc.

geost(+Objects,+Shapes)   since release 4.1
geost(+Objects,+Shapes,+Options)   since release 4.1
geost(+Objects,+Shapes,+Options,+Rules)   since release 4.1

constrains the location in space of non-overlapping multi-dimensional Objects, each of which taking a shape among a set of Shapes.

Each shape is defined as a finite set of shifted boxes, where each shifted box is described by a box in a k-dimensional space at the given offset with the given sizes. A shifted box is described by a ground term sbox(Sid,Offset,Size) where Sid, an integer, is the shape id; Offset, a list of k integers, denotes the offset of the shifted box from the origin of the object; and Size, a list of k integers greater than zero, denotes the size of the shifted box. Then, a shape is a collection of shifted boxes all sharing the same shape id. The shifted boxes associated with a given shape must not overlap. Shapes is thus the list of such sbox/3 terms.

Each object is described by a term object(Oid,Sid,Origin where Oid, an integer, is the unique object id; Sid, a domain variable, is the shape id; and Origin, a list of domain variables, is the origin coordinate of the object. If Sid is nonground, then the object is said to be polymorphic. The possible values for Sid are the shape ids that occur in Shapes. Objects is thus the list of such object/3 terms.

If given, then Options is a list of zero or more of the following, where Boolean must be true or false (false is the default):

lex(ListOfOid)

where ListOfOid should be a list of distinct object ids, denotes that the origin vectors of the objects according to ListOfOid should be in ascending lexicographic order. Multiple lex/1 options can be given, but should mention disjoint sets of objects.

cumulative(Boolean)

If true, then redundant reasoning methods are enabled, based on projecting the objects onto each dimension.

disjunctive(Boolean)

If true, then cliques of objects are detected that clash in one dimension and so must be separated in the other dimension. This method only applies in the 2D case.

longest_hole(Value,Maxbacks)

This method only applies in the 2D case and in the absence of polymorphic objects. Value can be all, true or false. If true, then the filtering algorithm computes and uses information about holes that can be tolerated without necessarily failing the constraint. If all,then more precise information is computed. If false, then no such information is computed. Maxbacks should be an integer >= -1 and gives a bound on the effort spent tightening the longest hole information. Experiments suggest that 1000 may be a reasonable compromise value.

parconflict(Boolean)

If true, then redundant reasoning methods are enabled, based on computing the number of items that can be put in parallel in the different dimensions.

visavis_init(Boolean)

If true, then a redundant method is enabled that statically detects placements that would cause too large holes. This method can be quite effective.

visavis_floating(Boolean)   obsolescent

Disabled, because it has not been shown to pay off experimentally except in rare cases.

visavis(Boolean)   obsolescent

Disabled, because it has not been shown to pay off experimentally.

corners(Boolean)   obsolescent

Disabled, because it has not been shown to pay off experimentally.

task_intervals(Boolean)   obsolescent

Disabled, because it has not been shown to pay off experimentally.

dynamic_programming(Boolean)

If true, then a redundant reasoning method is enabled that solves a 2D knapsack problem for every two adjacent columns of the projection of the objects onto each dimension. This method has pseudo-polynomial complexity but can be quite powerful.

polymorphism(Boolean)   obsolescent

Disabled, because it has not been shown to pay off experimentally.

pallet_loading(Boolean)

If true, and if all objects consist of a single shifted box of the same shape, modulo rotations, then a redundant method is enabled that recognizes necessary conditions for this special case.

overlap(Boolean)

If true, then the constraint that objects be non-overlapping is lifted. This option is useful mainly in conjunction with the Rules argument, in case the placement of objects should be restricted by the Rules only.

volume(Total)

If given, then Total is constrained to be the total volume of Objects.

bounding_box(Lower,Upper)

Lower=[L1,...,Lk] and Upper=[U1,...,Uk] should be lists of domain variables. The following conditions are imposed:

  • For every point P = [P1,...,Pk] occupied by an object, L1 <= P1 < U1, ..., Lk <= Pk < Uk.
  • For every j in 1..k, there exists a point P = [P1,...,Pj,...,Pk] occupied by an object such that Pj=Lj.
  • For every j in 1..k, there exists a point P = [P1,...,Pj,...,Pk] occupied by an object such that Pj=Uj-1.
fixall(Flag,Patterns)

If given, then Flag is a domain variable in 0..1. If Flag equals 1, then either initially or by binding Flag during search, the constraint switches behavior into greedy assignment mode. The greedy assignment will either succeed and assign all shape ids and origin coordinates to values that satisfy the constraint, or merely fail. Flag is never bound by the constraint; its sole function is to control the behavior of the constraint.

Greedy assignment is done one object at a time, in the order of Objects. The assignment per object is controlled by Patterns, which should be a list of one or more pattern terms of the form object(_,SidSpec,OriginSpec), where SidSpec is a term min(I) or max(I), OriginSpec is a list of k such terms, and I is a unique integer between 1 and k+1.

The meaning of the pattern is as follows. The variable in the position of min(1) or max(1) is fixed first; the variable in the position of min(2) or max(2) is fixed second; and so on. min(I) means trying values in ascending order; max(I) means descending order.

If Patterns contains m pattern, then object 1 is fixed according to pattern 1, …, object m is fixed according to pattern m, object m+1 is fixed according to pattern 1, and so on. For example, suppose that the following option is given: 

fixall(F, [object(_,min(1),[min(3),max(2)]),
           object(_,max(1),[min(2),max(3)])])

Then, if the program binds F to 1, then the constraint enters greedy assignment mode and endeavors to fix all objects as follows.

  • For object 1, 3, …, (a) the shape is fixed to the smallest possible value, (b) the Y coordinate is fixed to the largest possible value, (c) the X coordinate is fixed to the smallest possible value.
  • For object 2, 4, …, (a) the shape is fixed to the largest possible value, (b) the X coordinate is fixed to the smallest possible value, (c) the Y coordinate is fixed to the largest possible value.

If given, then Rules is a list of zero or more terms of the form shown below, and impose extra constraints on the placement of the objects. For the time being, the details are described in [Carlsson, Beldiceanu & Martin 08]. Please note: the rules require that all shapes of a polymorphic objects consist of the same number of shifted boxes. For example, Shapes = [sbox(1,[0,0],[3,1]),sbox(1,[0,1],[2,4]),sbox(2,[0,0],[3,1])] will not work.

sentence::=macro | fol
macro::=head ---> body
head::=term{ to be substituted by a body }
body::=term{ to substitute for a head }
fol::=#\ fol{ negation }
|fol #/\ fol{ conjunction }
|fol #\/ fol{ disjunction }
|fol #=> fol{ implication }
|fol #<=> fol{ equivalence }
|exists(var,collection,fol){ existential quantification }
|forall(var,collection,fol){ universal quantification }
|card(var,collection,integer,integer,fol){ cardinality }
|true
|false
|expr relop expr{ rational arithmetic }
|head{ macro application }
expr::=expr + expr
|- expr
|expr - expr
|min(expr,expr)
|max(expr,expr)
|expr * groundexpr
|groundexpr * expr
|expr / groundexpr
|attref
|integer
|fold(var,collection,fop,expr,expr)
|variable{ quantified variable }
|head{ macro application }
groundexpr::=expr{ where expr is ground }
attref::=entity ^ attr
attr::=term{ attribute name }
|variable{ quantified variable }
relop::=#< | #= | #> | #\= | #=< | #>=
fop::=+ | min | max
collection::=list
|objects(list){ list of oids }
|sboxes(list){ list of sids }

Corresponds to geost* in MiniZinc.

The following example shows geost/2 modeling three non-overlapping objects. The first object has four possible shapes, and the other two have two possible shapes each. 

| ?- domain([X1,X2,X3,Y1,Y2,Y3], 1, 4),
     S1 in 1..4,
     S2 in 5..6,
     S3 in 7..8,
     geost([object(1,S1,[X1,Y1]), 
            object(2,S2,[X2,Y2]),
            object(3,S3,[X3,Y3])],
           [sbox(1,[0,0],[2,1]), 
            sbox(1,[0,1],[1,2]), 
            sbox(1,[1,2],[3,1]),
            sbox(2,[0,0],[3,1]), 
            sbox(2,[0,1],[1,3]), 
            sbox(2,[2,1],[1,1]),
            sbox(3,[0,0],[2,1]), 
            sbox(3,[1,1],[1,2]), 
            sbox(3,[-2,2],[3,1]),
            sbox(4,[0,0],[3,1]), 
            sbox(4,[0,1],[1,1]), 
            sbox(4,[2,1],[1,3]),
            sbox(5,[0,0],[2,1]), 
            sbox(5,[1,1],[1,1]), 
            sbox(5,[0,2],[2,1]),
            sbox(6,[0,0],[3,1]), 
            sbox(6,[0,1],[1,1]), 
            sbox(6,[2,1],[1,1]),
            sbox(7,[0,0],[3,2]), 
            sbox(8,[0,0],[2,3])]).

The shapes are illustrated in the following picture:


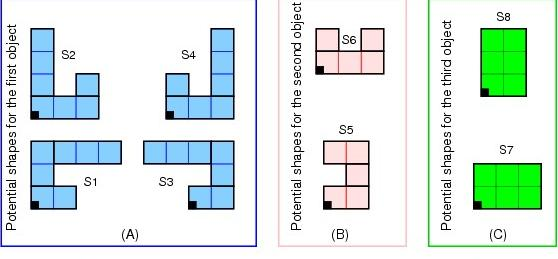
images/geost1a
geost/2: three objects and eight shapes

A ground solution is shown in the following picture:


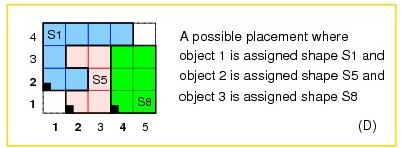
images/geost1b
geost/2: a ground solution

The following example shows how to encode in Rules “objects with oid 1, 2 and 3 must all be at least 2 units apart from objects with oid 4, 5 and 6”. 

[ (origin(O1,S1,D) ---> O1^x(D)+S1^t(D)),

  (end(O1,S1,D) ---> O1^x(D)+S1^t(D)+S1^l(D)),

  (tooclose(O1,O2,S1,S2,D) --->
      end(O1,S1,D)+2 #> origin(O2,S2,D) #/\
      end(O2,S2,D)+2 #> origin(O1,S1,D)),

  (apart(O1,O2) --->
      forall(S1,sboxes([O1^sid]),
          forall(S2,sboxes([O2^sid]),
              #\ tooclose(O1,O2,S1,S2,1) #\/
              #\ tooclose(O1,O2,S1,S2,2)))),

  (forall(O1,objects([1,2,3]),
      forall(O2,objects([4,5,6]), apart(O1,O2))))].

The following example shows how to encode in Rules “objects 3 and 7 model rooms that must be adjacent and have a common border at least 1 unit long”. 

[ (origin(O1,S1,D) ---> O1^x(D)+S1^t(D)),

  (end(O1,S1,D) ---> O1^x(D)+S1^t(D)+S1^l(D)),

  (overlap(O1,S1,O2,S2,D) --->
      end(O1,S1,D) #> origin(O2,S2,D) #/\
      end(O2,S2,D) #> origin(O1,S1,D)),

  (abut(O1,O2) --->
      forall(S1,sboxes([O1^sid]), 
          forall(S2,sboxes([O2^sid]),
              ((origin(O1,S1,1) #= end(O2,S2,1) #\/ 
                origin(O2,S2,1) #= end(O1,S1,1)) #/\ 
               overlap(O1,S1,O2,S2,2)) #\/
              ((origin(O1,S1,2) #= end(O2,S2,2) #\/ 
                origin(O2,S2,2) #= end(O1,S1,2)) #/\ 
               overlap(O1,S1,O2,S2,1))))),

  (forall(O1,objects([3]),
      forall(O2,objects([7]), abut(O1,O2))))].
Send feedback on this subject.