automaton(Signature, SourcesSinks, Arcs) since release 4.1automaton(Sequence, Template, Signature, SourcesSinks, Arcs, Counters, Initial, Final)automaton(Sequence, Template, Signature, SourcesSinks, Arcs, Counters, Initial, Final, Options) since release 4.1The arguments are described below in terms of their abstract syntax:
- Sequence
The sequence of terms of interest; abstract grammar category sequence.
- Template
A template for an item of the sequence; abstract grammar category template. Only relevant if some state transition involving counter arithmetic mentions a variable occurring in Template, in which case the corresponding term in a sequence element will be accessed.
- Signature
The signature of Sequence; abstract grammar category signature. The automaton is not driven by Sequence itself, but by Signature, which ranges over some alphabet, implicitly defined by the values used by Arcs. In addition to
automaton/[8,9], you must call a constraint that maps Sequence to Signature.- SourcesSinks
The source and sink nodes of the automaton; abstract grammar category sourcessinks.
- Arcs
The arcs (transitions) of the automaton; abstract grammar category arcs. Any transition not mentioned is assumed to go to an implicit failure node. An arc optionally contains expressions for updated counter values; by default, the counters remain unchanged. Conditional updates can be specified.
- Counters
A list of variables, local to the constraint; abstract grammar category counters.
- Initial
A list of initial values, usually instantiated; abstract grammar category initial.
- Final
A list of final values, usually uninstantiated; abstract grammar category final.
- Options
Abstract grammar category options; a list of zero or more of the following terms. All but the last option are implemented by adding auxiliary counters to the automaton including the necessary updates in the arcs:
valueprec(First,Later,N) since release 4.1.3-
N is unified with n, computed such that: if the value Later occurs in the Signature, then First occurs n times before the first occurrence of Later, otherwise n=0.
anystretchocc(N) since release 4.1.3-
N is unified with the number of (nonempty) stretches of any single value in the Signature.
stretchocc(ValuePat,N) since release 4.1.3-
N is unified with the number of stretches of values matching ValuePat (abstract grammar category valuepat) in the Signature.
stretchoccmod(ValuePat,Mod,N) since release 4.1.3-
N is unified with the number (modulo Mod) of stretches of values matching ValuePat (abstract grammar category valuepat) the Signature.
stretchmaxlen(ValuePat,N) since release 4.1.3-
N is unified with n, computed such that: if values matching ValuePat (abstract grammar category valuepat) occur the Signature, then n is the length of the longest such stretch, otherwise n=0.
stretchminlen(ValuePat,N) since release 4.1.3-
N is unified with n, computed such that: if values matching ValuePat (abstract grammar category valuepat) occur the Signature, then n is the length of the shortest such stretch, otherwise n is a large integer.
wordocc(WordPat,N) since release 4.1.3-
N is unified with the number of words matching WordPat (abstract grammar category wordpat) in the Signature.
wordoccmod(WordPat,Mod,N) since release 4.1.3-
N is unified with the number (modulo Mod) of words matching WordPat (abstract grammar category wordpat) in the Signature.
wordprefix(WordPat,ZO) since release 4.1.3-
If the prefix of the Signature matches WordPat (abstract grammar category wordpat), then ZO is unified with 1, otherwise with 0.
wordsuffix(WordPat,ZO) since release 4.1.3-
If the suffix of the Signature matches WordPat (abstract grammar category wordpat), then ZO is unified with 1, otherwise with 0.
state(Map,StateSequence) since release 4.1-
For a signature of length k, the constraint is implemented by decomposition into k smaller constraints mapping an old state to a new state. The states are represented as domain variables. StateSequence forms the list of these k+1 domain variables, starting with the initial state and ending with the final state. Map gives the interpretation of their values: it is a list of pairs Node-Value such that if the nth state variable Sn equals Value, then the automaton is in state Node having read n symbols.
counterseq(CounterSequence) since release 4.2.1-
Similarly to the list of states, CounterSequence forms the list of the k+1 instances of Counters, beginning with Initial and ending with Final.
Abstract syntax:
| sequence | ::= list of template | {all of which of the same shape} |
| template | ::= term | {most general shape of the sequence} |
| {its variables should be local to the constraint} | ||
| signature | ::= list of variable | |
| sourcessinks | ::= list of nodespec | |
| nodespec | ::= source(node) | {an initial state} |
| sink(node) | {an accept state} | |
| node | ::= term | |
| arcs | ::= list of arc | |
| arc | ::= arc(node,integer,node) | {from node, integer, to node} |
| arc(node,integer,node,exprs) | {exprs correspond to new counter values} | |
| arc(node,integer,node,conditional) | ||
| conditional | ::= (cond -> exprs) | |
| | (conditional ; conditional) | ||
| exprs | ::= list of Expr | {of same length as counters} |
| {Expr as defined in Syntax of Arithmetic Expressions} | ||
| {over counters, template and constants} | ||
| {variables occurring in counters correspond to old counter values} | ||
| {variables occurring in template refer to the current element of sequence} | ||
| cond | ::= constraint | {over counters, template and constants} |
{must be reifiable or true} | ||
| counters | ::= list of variable | {should be local to the constraint} |
| initial | ::= list of dvar | {of same length as counters} |
| final | ::= list of dvar | {of same length as counters} |
| option | ::= state(list of term,list of dvar) | |
| valueprec(integer,integer,dvar) | ||
| anystretchocc(dvar) | ||
| stretchocc(valuepat,dvar) | ||
| stretchoccmod(valuepat,dvar,integer) | ||
| stretchmaxlen(valuepat,dvar) | ||
| stretchminlen(valuepat,dvar) | ||
| wordocc(wordpat,dvar) | ||
| wordoccmod(wordpat,dvar,integer) | ||
| wordprefix(wordpat,dvar) | ||
| wordsuffix(wordpat,dvar) | ||
| valuepat | ::= integer | |
| | list of integer | {alternatives} | |
| valuepat/valuepat | {alternatives} | |
| wordpat | ::= list of valuepat | |
| dvar | ::= variable or integer |
If no counters are used, then the arguments Counters, Initial and
Final should be []. The arguments Template and
Sequence are only relevant if some Expr mentions a variable
in Template, in which case the corresponding position in
Sequence will be used at that point.
The constraint holds for a ground instance Sequence if:
- Signature is the signature corresponding to Sequence.
- The finite automaton encoded by SourcesSinks and Arcs stops in an accept state.
- Any counter arithmetic on the transitions map their Initial values to the Final values.
- Any extra constraint imposed by Options are true.
Here is an example. Suppose that you want to define the predicate
inflexion(N,L,Opt) which should hold if L
is a list of domain variables, and N is the number of times that
the sequence order switches between strictly increasing and strictly
decreasing. For example, the sequence [1,1,4,8,8,2,7,1] switches
order three times.
Such a constraint is conveniently expressed by a finite automaton over
the alphabet [<,=,>] denoting the order between consecutive list
elements. A counter is incremented when the order switches, and is
mapped to the first argument of the constraint. The automaton could
look as follows:
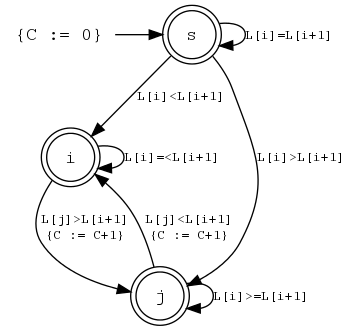
inflexion/3
The following piece of code encodes this using automaton/9. The
auxiliary predicate inflexion_signature/2 maps the sequence to a
signature where the consecutive element order is encoded over the
alphabet [0,1,2]. We use one counter with initial value 0 and
final value N (an argument of inflexion/3). Two
transitions increment the counter. All states are accept states.
inflexion(N, Vars, Opt) :-
inflexion_signature(Vars, Sign),
automaton(Sign, _, Sign,
[source(s),sink(i),sink(j),sink(s)],
[arc(s,1,s ),
arc(s,2,i ),
arc(s,0,j ),
arc(i,1,i ),
arc(i,2,i ),
arc(i,0,j,[C+1]),
arc(j,1,j ),
arc(j,0,j ),
arc(j,2,i,[C+1])],
[C],[0],[N],Opt).
inflexion_signature([], []).
inflexion_signature([_], []) :- !.
inflexion_signature([X,Y|Ys], [S|Ss]) :-
S in 0..2,
X #> Y #<=> S #= 0,
X #= Y #<=> S #= 1,
X #< Y #<=> S #= 2,
inflexion_signature([Y|Ys], Ss).
Some queries:
/* count the #inflections of a ground string */
| ?- inflexion(N, [1,1,4,8,8,2,7,1], []).
N = 3 ? RET
yes
/* find strings with two inflections */
| ?- length(L,4), domain(L,0,1),
inflexion(2,L,[]), labeling([],L).
L = [0,1,0,1] ? ;
L = [1,0,1,0] ? ;
no
/* find strings that are strictly increasing, strictly decreasing or all equal */
| ?- length(L,4), domain(L,0,3),
inflexion(I,L,[anystretchocc(1)]), labeling([],L).
I = 0,
L = [0,0,0,0] ? ;
I = 0,
L = [0,1,2,3] ? ;
I = 0,
L = [1,1,1,1] ? ;
I = 0,
L = [2,2,2,2] ? ;
I = 0,
L = [3,2,1,0] ? ;
I = 0,
L = [3,3,3,3] ? ;
no
/* find strings that contain an increase followed by a decrease */
| ?- length(L,4), domain(L,0,1),
inflexion(I,L,[wordocc([2,0],1)]), labeling([],L).
I = 1,
L = [0,0,1,0] ? ;
I = 1,
L = [0,1,0,0] ? ;
I = 2,
L = [0,1,0,1] ? ;
I = 2,
L = [1,0,1,0] ? ;
no
This constraint uses techniques from [Beldiceanu, Carlsson & Petit 04] and [Beldiceanu, Carlsson, Flener & Pearson 10].