smt(:ConstraintBody)The arithmetic, membership, and propositional constraints described
earlier are transformed at compile time to conjunctions of library
constraints. Although linear in the size of the source code, the
expansion of a propositional formula over reifiable constraints to
library goals can have time and memory overheads, and propagates
disjunctions very weakly. Temporary variables holding intermediate
values may have to be introduced, and the grain size of the constraint
solver invocations can be rather small. As an alternative to the
default propagation of such constraint formulas, this constraint is a
front-end to the case/[3,4] propagator, which treats such a
formula globally. The pruning can be stronger and it can run faster
than the default propagator, but this is not necessarily the case.
Bound-consistency is not guaranteed.
ConstraintBody should be of one of the following forms, or a propositional combination of such forms. See Syntax of Indexicals for the exact definition:
- var
inConstantRange element(var,CList,var)table([VList],CTable)- LinExpr RelOp LinExpr
- var {
Xstands forX#=1}
count(+Val,+List,+RelOp,?Count) deprecatedsum/3 constraint, one arithmetic
comparison, and several reified equalities.
count/4 maintains arc-consistency, but in practice, the
following constraint is a better alternative.
global_cardinality(+Xs,+Vals)global_cardinality(+Xs,+Vals,+Options)If either Xs or Vals is ground, and in many other
special cases, global_cardinality/[2,3] maintains
arc-consistency, but generally, bound-consistency cannot be
guaranteed. An arc-consistency algorithm [Regin 96] is used, roughly
linear in the total size of the domains.
Options is a list of zero or more of the following:
consistency(Cons)- Which filtering algorithm to use. One of the following:
domain- The constraint will use the algorithm mentioned above.
Implies
on(dom). The default. bound- The constraint will use the algorithm mentioned above.
Implies
on(minmax). value- The constraint will use a simple algorithm, which prevents too few or
too many of the Xs from taking values among the Vals.
Implies
on(val).
on(On)- How eagerly to wake up the constraint. One of the following:
dom- to wake up when the domain of a variable is changed (the default);
minmax- to wake up when the domain bound of a variable is changed;
val- to wake up when a variable becomes ground.
cost(Cost,Matrix)- Overrides any
consistency/1option value. A cost is associated with the constraint and reflected into the domain variable Cost. Matrix should be a d*n matrix of integers, represented as a list of d lists, each of length n. Assume that each Xi equals K(pi). The cost of the constraint is then Matrix[1,p1]+...+Matrix[d,pd].With this option, an arc-consistency algorithm [Regin 99] is used, the complexity of which is roughly O(d(m + n log n)) where m is the total size of the domains.
element(?X,+List,?Y)Maintains arc-consistency in X and
bound-consistency in List and Y.
Corresponds to nth1/3 in library(lists).
relation(?X,+MapList,?Y) deprecated-ConstantRange pairs, where the integer
keys occur uniquely (see Syntax of Indexicals). True if
MapList contains a pair X-R and Y
is in the range denoted by R.
An arbitrary binary constraint can be defined with relation/3.
relation/3 is implemented by straightforward transformation to
the following, more general constraint, with which arbitrary relations
can be defined compactly:
table(+Tuples,+Extension)table(+Tuples,+Extension,+Options)For convenience, Extension may contain ConstantRange (see Syntax of Indexicals) expressions in addition to integers.
Options is a list of zero or more of the following:
consistency(Cons)- This can be used to control the waking and pruning conditions of the constraint.
The value is one of the following:
domain- The constraint will maintain arc-consistency (the default).
bound- The constraint will maintain bound-consistency.
value- The constraint will wake up when a variable has become ground, and only prune a variable when its domain has been reduced to a singleton.
nodes(Nb)- Nb is unified with the number of DAG nodes.
order(Order)- Determines the variable order of the DAG. The following values are valid:
leftmost- The order is the one given in the arguments (the default).
id3- Each tuple, and the columns of the extension, is permuted according to the heuristic that more discriminating columns should precede less discriminating ones.
method(Method)- Controls the way the DAG is generated from the extension, after permuting
it if
order(id3)was chosen. The following values are valid:noaux- Equivalent DAG nodes are merged until no further merger is possible.
aux- An auxiliary, first variable is introduced, denoting extension row number. Then equivalent DAG nodes are merged until no further merger is possible.
table/[2,3] is implemented in terms of
the following, more general constraint, with which arbitrary relations
can be defined compactly:
case(+Template, +Tuples, +Dag)case(+Template, +Tuples, +Dag, +Options)This constraint encodes an n-ary constraint, defined by extension and/or linear inequalities. It uses a DAG-shaped data structure where nodes corresponds to variables and every arc is labeled by an admissible interval for the node above it and optionally by linear inequalities. The variable order is fixed: every path from the root node to a leaf node should visit every variable exactly once, in the order in which they occur lexically in Template. The constraint is true for a single ground tuple if there is a path from the root node to a leaf node such that (a) each tuple element is contained in the corresponding Min..Max interval on the path, and (b) any encountered linear inequalities along the path are true. The constraint is true for a set of ground tuples if it is true for each tuple of the set. The details are given below.
Template is a nonground Prolog term, each variable of which should occur exactly once. Its variables are merely place-holders; they should not occur outside the constraint nor inside Tuples.
Tuples is a list of terms of the same shape as Template. They should not share any variables with Template.
Dag is a list of nodes of the form
node(ID,X,Children), where X is a
template variable, and ID should be an integer, uniquely
identifying each node. The first node in the list is the root
node.
Nodes are either internal nodes or leaf nodes. For an
internal node, Children is a list of terms
(Min..Max)-ID2 or
(Min..Max)-SideConstraints-ID2, where
ID2 is the ID of a child node, Min is an integer or the atom
inf (minus infinity), and Max is an integer or the atom
sup (plus infinity). For a leaf node, Children is a list
of terms (Min..Max) or
(Min..Max)-SideConstraints.
SideConstraints is a list of side constraints of the form
scalar_product(Coeffs, Xs, #=<, Bound),
where Coeffs is a list of length k of integers, Xs is
a list of length k of template variables, and Bound is
an integer.
Variables in Tuples for which their template variable counterparts are constrained by side constraints, must have bounded domains.
Options is a list of zero or more of the following. It can be used to control the waking and pruning conditions of the constraint.
on(Spec)- Specifies how eagerly the constraint should react to domain changes of X.
prune(Spec)- Specifies the extent to which the constraint should prune the domain of X.
Spec is one of the following, where X is a template variable:
dom(X)- wake up when the domain of X has changed, resp. perform full
pruning on X. This is the default for all variables
mentioned in the constraint. In the absence of inequalities, full
pruning means arc-consistency.
min(X)- wake up when the lower bound of X has changed, resp.
prune only the lower bound of X.
max(X)- wake up when the upper bound of X has changed, resp.
prune only the upper bound of X.
minmax(X)- wake up when the lower or upper bound of X has changed, resp.
prune only the bounds of X. In the absence of inequalities,
this means bound-consistency.
val(X)- wake up when X has become ground, resp. only prune X
when its domain has been reduced to a singleton.
none(X)- ignore domain changes of X, resp. never prune X.
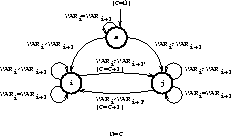
For example, recall that element(X,L,Y) wakes
up when the domain of X or the lower or upper bound of Y has
changed, performs full pruning of X, but only prunes the bounds of
Y. The following two constraints:
element(X, [1,1,1,1,2,2,2,2], Y),
element(X, [10,10,20,20,10,10,30,30], Z)
can be replaced by the following single constraint, which is equivalent declaratively as well as wrt. pruning and waking.
elts(X, Y, Z) :-
case(f(A,B,C), [f(X,Y,Z)],
[node(0, A,[(1..2)-1,(3..4)-2,(5..6)-3,(7..8)-4]),
node(1, B,[(1..1)-5]),
node(2, B,[(1..1)-6]),
node(3, B,[(2..2)-5]),
node(4, B,[(2..2)-7]),
node(5, C,[(10..10)]),
node(6, C,[(20..20)]),
node(7, C,[(30..30)])],
[on(dom(A)),on(minmax(B)),on(minmax(C)),
prune(dom(A)),prune(minmax(B)),prune(minmax(C))]).
The DAG of the previous example has the following shape:
elts/3.A couple of sample queries:
| ?- elts(X, Y, Z).
X in 1..8,
Y in 1..2,
Z in 10..30
| ?- elts(X, Y, Z), Z #>= 15.
X in(3..4)\/(7..8),
Y in 1..2,
Z in 20..30
| ?- elts(X, Y, Z), Y = 1.
Y = 1,
X in 1..4,
Z in 10..20
As an example with side constraints, consider assigning tasks to machines with given unavailibility periods. In this case, one can use a calendar constraint [CHIP 03, Beldiceanu, Carlsson & Rampon 05] to link the real origins of the tasks (taking the unavailibility periods into account) with virtual origins of the tasks (not taking the unavailibility periods into account). One can then state machine resource constraints using the virtual origins, and temporal constraints between the tasks using the real origins.
Assume, for example, three machines with unavailibility periods given by the following table:
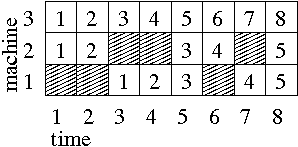
Machine 1 is not available during (real) time periods 1-2
and 6-6, machine 2 is not available during (real) time
periods 3-4 and 7-7, and machine 3 is always
available.
The following can then be used to express a calendar constraint for a
given task scheduled on machine M in 1..3, with virtual
origin V in 1..8, and real origin R in 1..8:
calendar(M, V, R) :-
M in 1..3,
V in 1..8,
R in 1..8,
smt((M#=1 #/\ V in 1..3 #/\ R#=V+2) #\/
(M#=1 #/\ V in 4..5 #/\ R#=V+3) #\/
(M#=2 #/\ V in 1..2 #/\ R#=V) #\/
(M#=2 #/\ V in 3..4 #/\ R#=V+2) #\/
(M#=2 #/\ V in 5..5 #/\ R#=V+3) #\/
(M#=3 #/\ R#=V)).
or equivalently as:
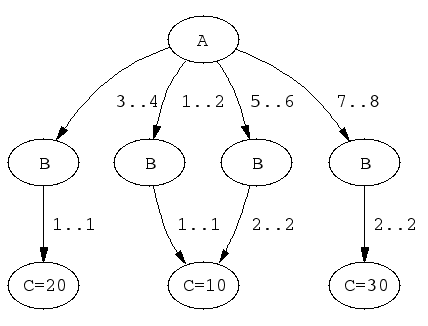
calendar(M, V, R) :-
case(f(A,B,C),
[f(M,V,R)],
[node(0, A, [(1..1)-1, (2..2)-2, (3..3)-3]),
node(1, B, [(1..3)-[scalar_product([1,-1],[B,C],#=<,-2),
scalar_product([1,-1],[C,B],#=<, 2)]-4,
(4..5)-[scalar_product([1,-1],[B,C],#=<,-3),
scalar_product([1,-1],[C,B],#=<, 3)]-4]),
node(2, B, [(1..2)-[scalar_product([1,-1],[B,C],#=<, 0),
scalar_product([1,-1],[C,B],#=<, 0)]-4,
(3..4)-[scalar_product([1,-1],[B,C],#=<,-2),
scalar_product([1,-1],[C,B],#=<, 2)]-4,
(5..5)-[scalar_product([1,-1],[B,C],#=<,-3),
scalar_product([1,-1],[C,B],#=<, 3)]-4]),
node(3, B, [(1..8)-[scalar_product([1,-1],[B,C],#=<, 0),
scalar_product([1,-1],[C,B],#=<, 0)]-4]),
node(4, C, [(1..8)])]).
Note that equality must be modeled as the conjunction of inequalities,
as only constraints of the form scalar_product(+Coeffs,
+Xs, #=<, +Bound) are allowed as side constraints.
The DAG of the calendar constraint has the following shape:
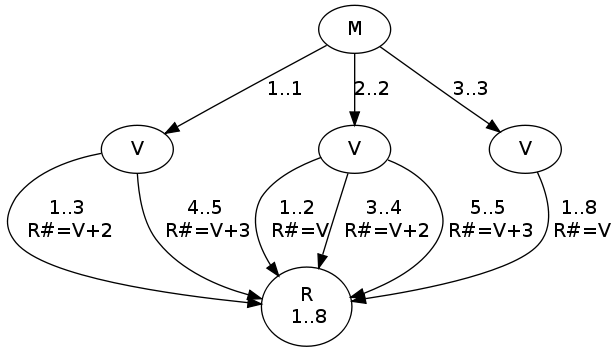
calendar/3.A couple of sample queries:
| ?- M in 1..3, V in 1..8, R in 1..8, calendar(M, V, R).
M in 1..3,
V in 1..8,
R in 1..8
| ?- M in 1..3, V in 1..8, R in 1..8, calendar(M, V, R), M #= 1.
M = 1,
V in 1..5,
R in(3..5)\/(7..8)
| ?- M in 1..3, V in 1..8, R in 1..8, calendar(M, V, R), M #= 2, V #> 4.
M = 2,
V = 5,
R = 8
all_different(+Variables)all_different(+Variables, +Options)all_distinct(+Variables)all_distinct(+Variables, +Options)Options is a list of zero or more of the following:
consistency(Cons)- Which algorithm to use, one of the following:
domain- The default for
all_distinct/[1,2]andassignment/[2,3]. an arc-consistency algorithm [Regin 94] is used, roughly linear in the total size of the domains. Implieson(dom). bound- a bound-consistency algorithm [Mehlhorn 00] is used. This algorithm
is nearly linear in the number of variables and values.
Implies
on(minmax). value- The default for
all_different/[1,2]. An algorithm achieving exactly the same pruning as a set of pairwise inequality constraints is used, roughly linear in the number of variables. Implieson(val).
on(On)- How eagerly to wake up the constraint. One of the following:
dom- (the default for
all_distinct/[1,2]andassignment/[2,3]), to wake up when the domain of a variable is changed; min- to wake up when the lower bound of a domain is changed;
max- to wake up when the upper bound of a domain is changed;
minmax- to wake up when some bound of a domain is changed;
val- (the default for
all_different/[1,2]), to wake up when a variable becomes ground.
nvalue(?N, +Variables)all_distinct/2.