count(+Val,+List,+RelOp,?Count)
where Val is an integer, List is a list of integers or
domain variables, Count an integer or a domain
variable, and RelOp is a relational symbol as in
Arithmetic Constraints. True if N is the number of elements
of List that are equal to Val and N RelOp Count.
Thus, count/4 is a generalization of exactly/3 (not an
exported constraint), which was used in an example earlier.
count/4 maintains domain-consistency, but in practice, the
following constraint is a better alternative.
global_cardinality(+Xs,+Vals)
global_cardinality(+Xs,+Vals,+Options)
where Xs = [X_1,\ldots,X_d] is a list of integers or domain variables, and Vals = [K_1-V_1,\ldots,K_n-V_n] is a list of pairs where each key K_i is a unique integer and V_i is a domain variable or an integer. True if every element of Xs is equal to some key and for each pair K_i-V_i, exactly V_i elements of Xs are equal to K_i.
If either Xs or Vals is ground, and in many other
special cases, global_cardinality/[2,3] maintains
domain-consistency, but generally, interval-consistency cannot be
guaranteed. A domain-consistency algorithm [Regin 96] is used, roughly
linear in the total size of the domains.
Options is a list of zero or more of the following:
cost(Cost,Matrix)- A cost is associated with the constraint and reflected into the domain
variable Cost. Matrix should be a d\times n
matrix, represented as a list of d lists, each of
length n. Assume that each X_i equals K_p_i.
The cost of the constraint is then
\Matrix[1,p_1]+\cdots+\Matrix[d,p_d].
With this option, a domain-consistency algorithm [Regin 99] is used, the complexity of which is roughly O(d(m + n \log n)) where m is the total size of the domains.
element(?X,+List,?Y)
where X and Y are integers or domain variables and List is a list of integers or domain variables. True if the X:th element of List is Y. Operationally, the domains of X and Y are constrained so that for every element in the domain of X, there is a compatible element in the domain of Y, and vice versa.
This constraint uses an optimized algorithm for the special case where List is ground.
element/3 maintains domain-consistency in X and
interval-consistency in List and Y.
relation(?X,+MapList,?Y)
where X and Y are integers or domain variables and
MapList is a list of
integer-ConstantRange pairs, where the integer
keys occur uniquely (see Syntax of Indexicals). True if
MapList contains a pair X-R and Y
is in the range denoted by R.
Operationally, the domains of X and Y are constrained so that for every element in the domain of X, there is a compatible element in the domain of Y, and vice versa.
If MapList is not ground, the constraint must be wrapped in
call/1 to postpone goal expansion until runtime.
An arbitrary binary constraint can be defined with relation/3.
relation/3 is implemented in terms of the following, more
general constraint, with which arbitrary relations can be defined compactly:
case(+Template, +Tuples, +Dag)
case(+Template, +Tuples, +Dag, +Options)
Template is an arbitrary non-ground Prolog term. Its variables are merely place-holders; they should not occur outside the constraint nor inside Tuples.
Tuples is a list of terms of the same shape as Template. They should not share any variables with Template.
Dag is a list of nodes of the form
node(ID,X,Successors), where X is a
place-holder variable. The set of all X should equal the
set of variables in Template. The first node in the
list is the root node. Let rootID denote its ID.
Nodes are either internal nodes or leaf nodes. In the
former case, Successors is a list of terms
(Min..Max)-ID2, where the ID2 refers to a
child node. In the latter case, Successors is a list of
terms (Min..Max). In both cases, the
(Min..Max) should form disjoint intervals.
ID is a unique, integer identifier of a node.
Each path from the root node to a leaf node corresponds to one set of tuples admitted by the relation expressed by the constraint. Each variable in Template should occur exactly once on each path, and there must not be any cycles.
Options is a list of zero or more of the following. It can be used to control the waking and pruning conditions of the constraint, as well as to identify the leaf nodes reached by the tuples:
leaves(TLeaf,Leaves)- TLeaf is a place-holder variable. Leaves is a
list of variables of the same length as Tuples. This
option effectively extends the relation by one argument,
corresponding to the ID of the leaf node reached by a particular tuple.
on(Spec)- Specifies how eagerly the constraint should react to domain changes of X.
prune(Spec)- Specifies the extent to which the constraint should prune the domain of X.
Spec is one of the following, where X is a place-holder variable occurring in Template or equal to TLeaf:
dom(X)- wake up when the domain of X has changed, resp. perform full
pruning on X. This is the default for all variables
mentioned in the constraint.
min(X)- wake up when the lower bound of X has changed, resp.
prune only the lower bound of X.
max(X)- wake up when the upper bound of X has changed, resp.
prune only the upper bound of X.
minmax(X)- wake up when the lower or upper bound of X has changed, resp.
prune only the bounds of X.
val(X)- wake up when X has become ground, resp. only prune X
when its domain has been narrowed to a singleton.
none(X)- ignore domain changes of X, resp. never prune X.
The constraint holds if path(rootID,Tuple,Leaf) holds for each Tuple in Tuples and Leaf is the corresponding element of Leaves if given (otherwise, Leaf is a free variable).
path(ID,Tuple,Leaf) holds if Dag contains a term
node(ID,Var,Successors), Var is the
unique k:th element of Template, i is the k:th
element of Tuple, and:
- The node is an internal node, and
- Successors contains a term
(Min..Max)-Child, - \Min \leq i \leq \Max, and
- path(Child,Tuple,Leaf) holds; or
- Successors contains a term
- The node is a leaf node, and
- Successors contains a term
(Min..Max), - \Min \leq i \leq \Max, and Leaf = ID.
- Successors contains a term
For example, recall that element(X,L,Y) wakes
up when the domain of X or the lower or upper bound of Y has
changed, performs full pruning of X, but only prunes the bounds of
Y. The following two constraints:
element(X, [1,1,1,1,2,2,2,2], Y),
element(X, [10,10,20,20,10,10,30,30], Z)
can be replaced by the following single constraint, which is equivalent declaratively as well as wrt. pruning and waking. The fourth argument illustrates the leaf feature:
elts(X, Y, Z, L) :-
case(f(A,B,C), [f(X,Y,Z)],
[node(0, A,[(1..2)-1,(3..4)-2,(5..6)-3,(7..8)-4]),
node(1, B,[(1..1)-5]),
node(2, B,[(1..1)-6]),
node(3, B,[(2..2)-5]),
node(4, B,[(2..2)-7]),
node(5, C,[(10..10)]),
node(6, C,[(20..20)]),
node(7, C,[(30..30)])],
[on(dom(A)),on(minmax(B)),on(minmax(C)),
prune(dom(A)),prune(minmax(B)),prune(minmax(C)),
leaves(_,[L])]).
The DAG of the previous example has the following shape:
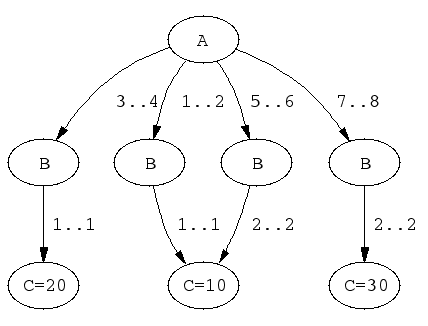
elts/4 | ?- elts(X, Y, Z, L).
L in 5..7,
X in 1..8,
Y in 1..2,
Z in 10..30
| ?- elts(X, Y, Z, L), Z #>= 15.
L in 6..7,
X in(3..4)\/(7..8),
Y in 1..2,
Z in 20..30
| ?- elts(X, Y, Z, L), Y = 1.
Y = 1,
L in 5..6,
X in 1..4,
Z in 10..20
| ?- elts(X, Y, Z, L), L = 5.
Z = 10,
X in(1..2)\/(5..6),
Y in 1..2
all_different(+Variables)
all_different(+Variables, +Options)
all_distinct(+Variables)
all_distinct(+Variables, +Options)
where Variables is a list of domain variables with bounded domains or integers. Each variable is constrained to take a value that is unique among the variables. Declaratively, this is equivalent to an inequality constraint for each pair of variables.
Options is a list of zero or more of the following:
on(On)- How eagerly to wake up the constraint. One of:
dom- (the default for
all_distinct/[1,2]andassignment/[2,3]), to wake up when the domain of a variable is changed; min- to wake up when the lower bound of a domain is changed;
max- to wake up when the upper bound of a domain is changed;
minmax- to wake up when some bound of a domain is changed;
val- (the default for
all_different/[1,2]), to wake up when a variable becomes ground.
consistency(Cons)- Which algorithm to use, one of:
global- The default for
all_distinct/[1,2]andassignment/[2,3]. A domain-consistency algorithm [Regin 94] is used, roughly linear in the total size of the domains. local- The default for
all_different/[1,2]. An algorithm achieving exactly the same pruning as a set of pairwise inequality constraints is used, roughly linear in the number of variables. bound- An interval-consistency algorithm [Mehlhorn 00] is used. This algorithm is nearly linear in the number of variables and values.